Movimiento circular uniforme.

Un caso particular de movimiento en dos dimensiones es el de una partícula que se mueve describiendo una trayectoria en una circunferencia, con velocidad . Si la rapidez Ves constante, se llama Movimiento Circular Uniforme . En el mundo cotidiano, es frecuente observar las trayectorias curvas que describen algunos cuerpos en su movimiento continuo. Cuando una partícula se mueve según una trayectoria curva debe tener una componente de la aceleración perpendicular a dicha trayectoria, incluso si su rapidez es constante. Para una trayectoria circular existe una relación sencilla entre la componente normal de la aceleración, la rapidez de la partícula y el radio de la trayectoria. Un satélite espacial que gira en torno a la Tierra o el hecho de que ésta gire alrededor del Sol son ejemplos en una trayectoria circular. El objetivo es aprender a describir este tipo de movimientos. 

Definición

Para estudiar un movimiento como éste es necesario definir el vector velocidad en cada instante; Se debe conocer su módulo o magnitud, la dirección de que es la recta tangente a la trayectoria en el punto que la partícula ocupa en el instante considerado, y su sentido es del movimiento de la partícula en ese instante.

 El sentido y dirección de cambian constantemente ya que varían la dirección y sentido de la tangente a la curva. Un cuerpo se moverá según una trayectoria curva, siempre y cuando la aceleración existente en el cuerpo tenga una componente perpendicular a la dirección del movimiento.

Esta aceleración perpendicular a la velocidad se denomina aceleración centrípeta () y está siempre dirigida hacia el centro de la trayectoria. Esta aceleración también suele recibir el nombre de aceleración radial< oaceleración normal<, pues tiene la dirección del radio de curvatura de la trayectoria en el punto dado, y apunta hacia el centro de la curva. 

Velocidad tangencial y velocidad angular.

Velocidad Tangencial o Lineal:

En un MCU la velocidad tangencial cambia continuamente de dirección y sentido, pero la rapidez es constante porque la longitud del vector velocidad tangencial no varía.

Si se tiene un objeto físico cualquiera que describe circunferencias de centro O y radio r, con MCU en el sentido contrario del movimiento de las agujas del Reloj, la velocidad tangencial o lineal es aquella que tiene el objeto físico en un instante cualquiera del movimiento circular. 

Se representa por un vector tangente a la circunferencia en el punto que se considere. Se puede observar que en el MCU la velocidad tangencial o lineal no es constante, pues el vector que representa dicha velocidad cambia continuamente de dirección y sentido. El módulo de la velocidad tangencial en MCU se mide por el cociente entre el arco descrito por el móvil y el tiempo empleado en recorrerlo. 

Velocidad Angular: 

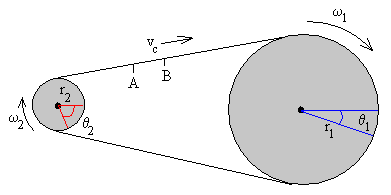
Se considera un objeto físico que describe circunferencias de centro O y radio r con MCU. Si en un intervalo de tiempo t el objeto físico pasa de la posición A a la posición B describiendo el arco AB y el radio r barre el ángulo . Como tiene su vértice en el centro de la circunferencia, se cumple que la medida del ángulo  es igual a la medida del arco AB. 

  Por consiguiente, si el objeto físico describe áreas iguales, se tendrá que el radio r barre ángulos iguales en tiempo iguales, por lo que se habla de una Velocidad Angular del objeto físico. Una característica que distingue a este tipo de movimientos es que el ángulo que recorre una partícula por unidad de tiempo es constante, por lo que su velocidad angular es constante

La velocidad angular en un movimiento circular uniforme se mide por el cociente entre el ángulo recorrido por el radio y el tiempo empleado en barrerlo. Designando la velocidad angular por la letra griega ? (omega) se tiene 

Un Radián es un ángulo central de una circunferencia que intercepta un arco de dicha circunferencia, cuya longitud es igual al radio de la misma.
Si se quiere determinar a cuántos radianes equivale un ángulo cualquiera  basta calcular cuantas veces cabe la longitud del radio en la longitud del arco.
Si la longitud del arco es L y la longitud del radio es r se tiene que: